La Regla de Bayes funciona a partir del cómputo de probabilidades. Como ya se discutió en el capítulo anterior, toda Probabilidad (\(p(x)\)) se define como un número real entre \(0\) y \(1\) que representa el grado de certidumbre que se tiene sobre la ocurrencia de un evento (\(x\)). En su definición más simple, la probabilidad puede computarse a partir de la razón entre el número de casos que incluyen al evento \(x\) y el total de casos que es posible de observar.
Derivación del Teorema de Bayes
Para calcular la Probabilidad Condicional de un evento \(A\) dada cierta evidencia \(B\), de tal forma que podamos saber si nuestra certidumbre ha incrementado o decrecido, y cuánto, tenemos la siguiente ecuación:
\[
\begin{equation}
p(A|B) = \frac{p(A \cap B)}{p(B)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)
\end{equation}
\]
La Ecuación 1 captura un razonamiento bastante intuitivo: Si queremos saber qué tan probable es el evento \(A\) dado que estoy usando la ocurrencia de \(B\) como referencia, primero hay que considerar la probabilidad de que ambos eventos aparezcan simultáneamente en el mundo (\(p(A \cap B)\)) y sopesar dicha probabilidad en relación a la probabilidad de que el evento \(B\) aparezca en el mundo (\(p(B)\)), independientemente de su relación con \(A\).
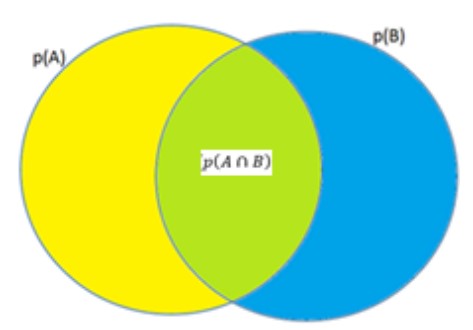
El diagrama de Venn que se muestra en la Figura 1 presenta el problema al que nos enfrentamos de manera gráfica: Imaginemos que estamos interesados en saber qué tan probable es el evento \(A\) una vez que hemos observado que ocurrió el evento \(B\). Antes de observar \(B\), tenemos una idea de cuál es la probabilidad de que ocurra \(A\), (\(p(A)\) , el área del círculo amarillo). Ahora, lo que nos interesa es utilizar la ocurrencia de \(B\) como una referencia para actualizar nuestro estimado inicial, (\(p(A|B)\)). Si sabemos que los eventos \(A\) y \(B\) suelen presentarse juntos en el mundo con cierta probabilidad, (\(p(A \cap B)\), el área verde donde ambos círculos se intersectan), necesitamos saber cuál es la probabilidad de que el evento observado \(B\) pertenezca a dicha área de intersección (en cuyo caso, anunciaría la ocurrencia simultánea de \(A\)), en relación a su probabilidad marginal (\(p(B)\), el área total del círculo azul). Para ello, tenemos que obtener la razón entre el área de \(B\) que intersecta a \(A\) (la probabilidad conjunta de \(A\) y \(B\)) y el área total de \(B\) (la probabilidad marginal de \(B\)). La Ecuación 2 captura este razonamiento, llevándonos de vuelta a la Ecuación 1 previamente expuesta.
\[
\begin{equation}
p(A|B) = \frac{\text{Probabilidad Conjunta A y B}}{\text{Probabilidad Marginal B}} = \frac{p(A \cap B)}{p(B)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)
\end{equation}
\]
De acuerdo a las Leyes de la Probabilidad, la probabilidad conjunta de dos eventos \(A\) y \(B\) se puede computar con la siguiente ecuación:
\[
p(A \cap B) = p(A) \cdot p(B|A) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3)
\]
Si insertamos la Ecuación 3 en el numerador de la Ecuación 2, obtenemos una ecuación que nos permite calcular la probabilidad de un evento \(A\) dada la observación de cierta evidencia \(B\). La ecuación resultante es el Teorema de Bayes.
\[
\begin{equation}
p(A|B) = \frac{p(A \cap B)}{p(B)} = \frac{p(A) \cdot p(B|A)}{p(B)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)
\end{equation}
\]
Las Ecuaciones 3 y 4 permiten enfatizar una diferencia importante en términos de la información que podemos extraer sobre la posible ocurrencia de \(A\) tras la observación de \(B\), dependiendo de si \(A\) y \(B\) están o no definidos como eventos independientes. De acuerdo a la relación previamente especificada en términos de la igualdad entre la probabilidad condicional y la probabilidad marginal, tendríamos que:
Si al tratarse de eventos independientes \(p(B|A) = p(B)\) y \(p(A|B) = p(A)\), entonces:
\[\begin{align}
p(A \cap B) &= p(A) \cdot p(B|A) \\
&= p(A) \cdot p(B) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5)
\end{align}\]
La Ecuación 5, que no es más que otra forma de expresar la ecuación general que define las probabilidades conjuntas para el caso específico en que los eventos a evaluar son independientes, es de hecho identificada dentro de las leyes de la probabilidad como aquella que describe ‘la probabilidad conjunta de eventos independientes’.
Finalmente, si sustituimos la Ecuación 5 en el Teorema de Bayes, reafirmamos formalmente que, dada su independencia, la observación de un evento \(A\) o \(B\), no proporciona información adicional sobre la ocurrencia del otro:
\[
\begin{equation}
p(A|B) = \frac{p(A \cap B)}{p(B)} = \frac{p(A) \cdot p(B)}{p(B)} = p(A)
\end{equation}
\]
Una vez desglosada la estructura y función de la Regla de Bayes, conviene familiarizarnos con la nomenclatura utilizada para referirnos a cada uno de los términos incluidos en el Teorema.
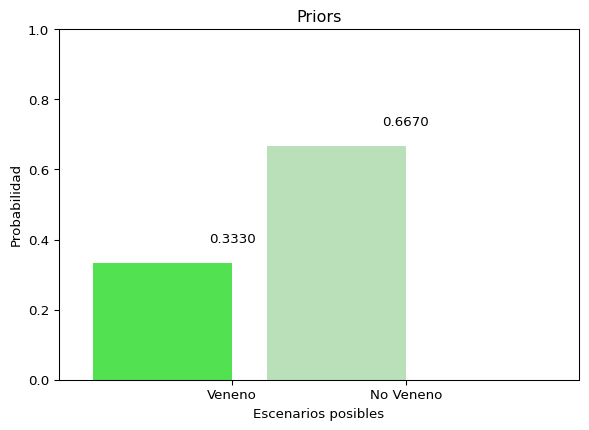
- La probabilidad prior ~ \(p(A)\)
Al estimado inicial que tenemos sobre la probabilidad de ocurrencia del evento de interés \(A\), antes de ver cualquier evidencia, se le conoce como probabilidad prior.
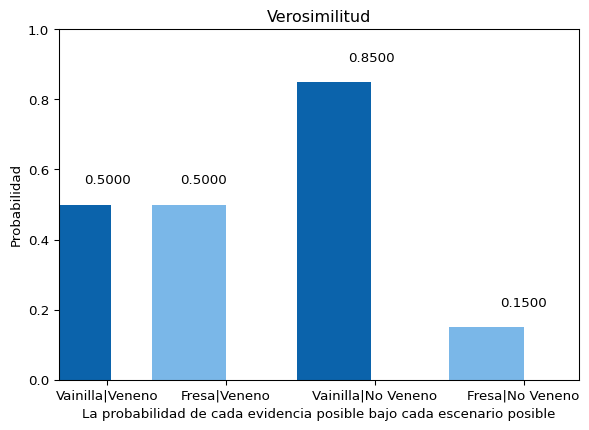
- La verosimilitud ~ \(p(B|A)\)
En el numerador del Teorema de Bayes, encontramos dos términos que al multiplicarse representan la probabilidad conjunta de ocurrencia del evento de interés \(A\) y la evidencia B. Uno de ellos corresponde a la probabilidad prior; el segundo, se expresa como la probabilidad condicional de observar la evidencia \(B\) cuando el evento de interés \(A\) de hecho ocurre. \(A\) esta segunda probabilidad condicional, se le conoce como verosimilitud. Tal como su nombre sugiere, la verosimilitud nos proporciona un indicador de la relación entre la evidencia \(B\) y el evento \(A\), a partir de un razonamiento inverso: Cuando \(A\) de hecho ocurre, ¿con qué probabilidad aparece en compañía de \(B\)? Es importante enfatizar que, contrario a lo que la intuición podría sugerir, las dos probabilidades condicionales implicadas en el Teorema de Bayes no son equivalentes. Es decir:
\[
p(A|B) \neq p(B|A)
\]
Esta relación suele quedar más clara si lo pensamos en términos de un ejemplo concreto: Imaginemos que estamos interesados en estimar la probabilidad de que llueva hoy, dado que vemos el cielo nublado. Hacernos esta pregunta tiene sentido, porque existe incertidumbre respecto a la posibilidad de que llueva, que puede reducirse sabiendo si el cielo está o no nublado. Sin embargo, sería extraño que nos preguntáramos si el cielo está nublado dado que escuchamos la lluvia caer, ya que sabemos que siempre que llueve es porque hay nubes en el cielo descargando agua. De tal forma que:
\[
p(\text{Lluvia}|\text{Cielo Nublado}) \neq p(\text{Cielo Nubaldo}|\text{Lluvia})
\]
A primera vista, puede parecer confuso que el cálculo de una probabilida condicional dependa de nuestro conocimiento de una segunda probabilidad condicional. Sin embargo, estimar la verosimilitud no es tan complicado una vez que se conoce la estructura del entorno en que situamos nuestra predicción. Por ejemplo, regresando al ejemplo anterior, sabemos que la verosimilitud que relaciona el cielo nublado con los días lluviosos tiene un valor de 1.
\[
p(\text{Cielo Nubaldo}|\text{Lluvia}) = 1
\]
- La verosimilitud Marginal ~ \(p(B)\)
A la probabilidad marginal de observar el evento \(B\) que estamos tomando como referencia para estimar la probabilidad de ocurrencia de \(A\), la conocemos como verosimilitud marginal. La verosimilitud marginal se define formalmente de la siguiente forma:
\[
p(B) = \sum_i p(A_i) \cdot p(B|A_i) = \sum_i p(A_i \cap B) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6)
\]
La Ecuación 6 define la verosimilitud marginal como una sumatoria de probabilidades conjuntas. Tal y como lo hemos manejado hasta ahora, A corresponde al Evento cuya probabilidad interesa calcular y \(B\) a la evidencia que estamos observando y con base en la cual hacemos el cómputo. El subíndice \(i\), indica que la sumatoria puede extenderse a tanta probabilidades conjuntas como eventos nos interese estimar (\(\{A_1, A_2, \dots, A_n\}\)). Por ejemplo, si interesa estimar la probabilidad de un solo evento \(A\), identificamos la no ocurrencia de \(A\) (\(\overline{A}\)) como la única alternativa posible. Entonces, la verosimilitud marginal se obtiene sumando la probabilidad conjunta de los eventos \(A\) y \(B\) (\(B \cap A\)), y la probabilidad conjunta de que se observe la evidencia \(B\) en ausencia de \(A\) (\(B \cap \overline{A}\)):
\[
p(B) = (p(A) \cdot p(B|A)) + (p(\overline{A}) \cdot p(B|\overline{A})) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7)
\]
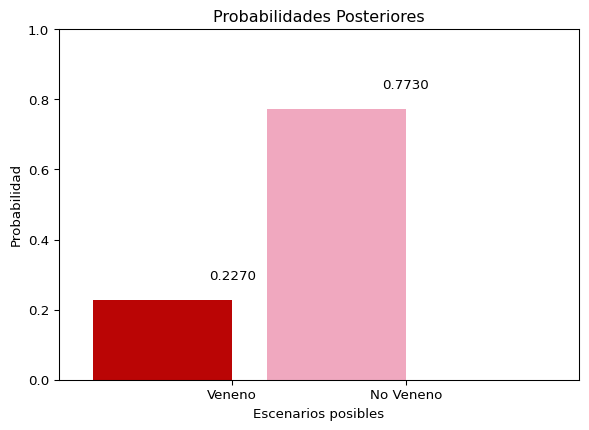
- La probabilidad posterior ~ \(p(A|B)\)
Al estimado final de la probabilidad de ocurrencia del evento \(A\), una vez habiendo ponderado la información aportada por la evidencia \(B\), se le conoce como probabilidad posterior.
\[
\begin{align}
p(A|B) &= \frac{p(A) \cdot p(B|A)}{p(B)} \\
\text{Probabilidad Posterior} &= \frac{\text{prior} \cdot \text{verosimilitud}}{\text{verosimilitu marginal}}
\end{align}
\]
Una vez entendiendo para qué sirve el Teorema de Bayes, cómo funciona y qué reglas de la probabilidad sigue, y habiendo identificado las ‘etiquetas’ dadas a cada uno de los términos que le componen, ¡Felicidades! Ya estás hablando en ‘Bayes’.