```{python}
import numpy as np
import matplotlib.pyplot as plt
import math
import ipywidgets as widgets
%matplotlib inline
def direct_actor(r_mean = 1, trials = 50, beta = 2, epsilon = 0.05, rb = 20, ry = 15):
mb = 0 # Action value for blue flower. choice = 0
my = 0 # Action value for yellow flower. choice = 1
evo_mb = [0] # Update in each time of blue flower's action value
evo_my = [0] # Update in each time of yellow flower's action value
evo_pb = [] # Update of probability to select Blue
evo_py = [] # Update of probability to select Yellow
e_rew = [0] # Expected reward (Function to find the maxima)
choices = [] # Record of choices made it.
for i in range(trials):
pb = math.exp(beta * mb) / (math.exp(beta * mb) + math.exp(beta * my))
py = math.exp(beta * my) / (math.exp(beta * mb) + math.exp(beta * my))
evo_pb.append(pb)
evo_py.append(py)
choice = np.random.choice(a = [0,1], p = [pb, py])
choices.append(choice)
if choice == 0:
mb = mb + epsilon * (1 - pb) * ( rb - r_mean)
my += -epsilon * py * ( ry - r_mean)
evo_mb.append(mb)
evo_my.append(my)
else:
mb = mb - epsilon * pb * (rb - r_mean)
my += epsilon * (1 - py) * (ry - r_mean)
evo_mb.append(mb)
evo_my.append(my)
e_r = rb * pb + ry*py
e_rew.append(e_r)
output = {'decision': np.array(choices), 'expected_reward': np.array(e_rew),
'action_value': [evo_mb, evo_my],'probability': [evo_pb, evo_py]}
return output
def direct_actor_simu(r_mean = 1, trials = 50, beta = 2, epsilon = 0.05, reward_blue = 20, reward_yellow = 10):
simu = direct_actor(r_mean, trials, beta, epsilon, reward_blue, reward_yellow)
# Choices
blues = simu['decision'] == 0
blues_cum = blues.cumsum()
yellows = simu['decision'] == 1
yellows_cum = yellows.cumsum()
# Action value.
value_mb = simu['action_value'][0]
value_my = simu['action_value'][1]
# Probabilities.
proba_blue = simu['probability'][0]
proba_yellow = simu['probability'][1]
# Reward Expected.
predi_rew = simu['expected_reward']
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(figsize = (15, 10), nrows = 2, ncols = 2)
# Ploting Choices
ax1.plot(blues_cum, color = '#73A4CA', lw = 2.5, ls = '--', alpha = 0.95, label = 'Choice: Blue')
ax1.plot(yellows_cum, color = '#F4D166', lw = 2.15, ls = '--', alpha = 0.75, label = 'Choice: Yellow')
ax1.set_ylabel(r'Sum visits', size = 12, labelpad = 3)
ax1.set_xlabel(r'Visits to flowers', size = 12, labelpad = 3)
ax1.tick_params(direction='inout', length = 7, width = 2 , colors='black',
grid_color='black', grid_alpha= 0.5, pad = 10, labelsize = 10)
ax1.legend( fontsize = 10)
# Ploting Action Value
ax2.plot(value_mb, color = '#73A4CA', lw = 2.5, ls = '-.', alpha = 0.95, label = 'Value: Blue')
ax2.plot(value_my, color = '#F4D166', lw = 2.15, ls = '-.', alpha = 0.75, label = 'Value: Yellow')
ax2.set_ylabel(r'$m$', size = 12, labelpad = 1)
ax2.set_xlabel(r'Visits to flowers', size = 12, labelpad = 3)
ax2.tick_params(direction='inout', length = 7, width = 2 , colors='black',
grid_color='black', grid_alpha= 0.5, pad = 10, labelsize = 10)
ax2.legend( fontsize = 10)
# Ploting Probability of Choice
ax3.plot(proba_blue, color = '#73A4CA', lw = 2.5, ls = '-', alpha = 0.95, label = 'Probability: Blue')
ax3.plot(proba_yellow, color = '#F4D166', lw = 2.15, ls = '-', alpha = 0.75, label = 'Probability: Yellow')
ax3.set_ylabel(r'Probability', size = 12, labelpad = 1)
ax3.set_xlabel(r'Visits to flowers', size = 12, labelpad = 3)
ax3.tick_params(direction='inout', length = 7, width = 2 , colors='black',
grid_color='black', grid_alpha= 0.5, pad = 10, labelsize = 10)
ax3.legend( fontsize = 10)
# Ploting Expected Reward
ax4.plot(predi_rew, color = '#4F9026', lw = 2.5, ls = ':', alpha = 0.95, label = '$E(r)$')
ax4.set_ylabel(r'Expected Reward $E(r)$', size = 12, labelpad = 1)
ax4.set_xlabel(r'Visits to flowers', size = 12, labelpad = 3)
ax4.tick_params(direction='inout', length = 7, width = 2 , colors='black',
grid_color='black', grid_alpha= 0.5, pad = 10, labelsize = 10)
ax4.legend( fontsize = 15)
plt.show()
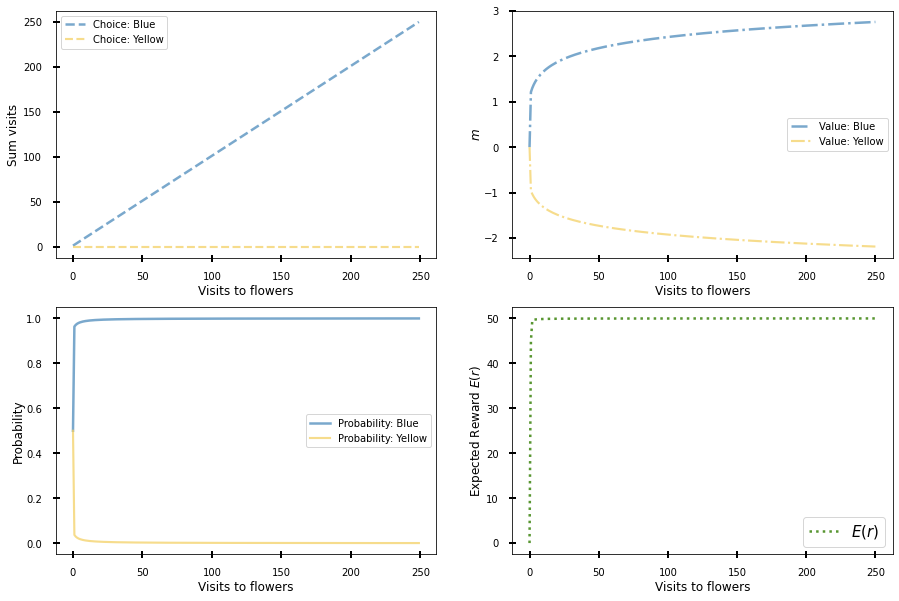
direct_actor_simu(r_mean = 1.5, trials = 250, beta = 1.5, epsilon = 0.05, reward_blue = 50, reward_yellow = 40)
```